实验员在挤压心脏的过程中,需要注意控制挤压的力度和时间。过度的挤压可能导致心肌损伤,而挤压时间过长则可能导致心肌坏死。因此,在实验过程中需要精确控制挤压的力度和时间,以确保实验结果的准确性和可靠性。心梗模型中的挤压心脏操作是一种重要的实验方法,可以帮助研究人员更好地了解心肌梗死的发生机制和病理生理过程。通过观察挤压心脏后的心脏功能变化和心肌损伤情况,研究人员可以进一步探讨心肌梗死的治*方法和预防措施。通过建立动物疾病模型,可以模拟人类疾病的发生和发展过程,进而评估药物的疗效和安全性。上海挤压心脏法心肌梗死(MI)模型
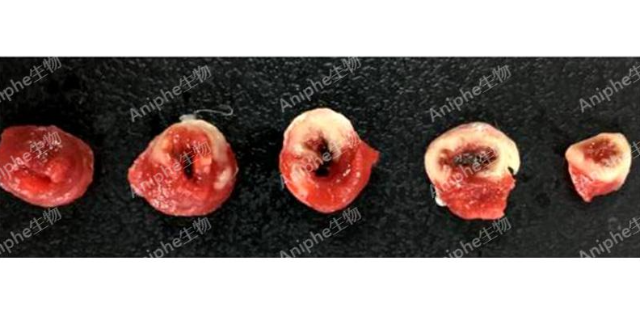
动物处死前,实验鼠麻醉后仰卧位固定,彻底暴露胸腔,将0.5%伊文斯蓝溶液经心尖部注入心腔,完毕后迅速取出心脏,反复用预冷的0.9%氯化钠溶液进行冲洗并剪除残留包膜及血管,用滤纸吸干水分。全心室心脏标本置于–20℃冷冻约30min后取出,在结扎线水平下将将左心室部分垂直长轴切成2-3mm的横断片,浸入2%TTC磷酸缓冲液中,置入37℃水浴反应30分钟。用4%的甲醛固定24h,以增强染色颜色对比,对切片进行扫描拍照。正常心肌染成蓝色,缺血心肌染成砖红色,梗死心肌不着色。南京大小鼠心肌梗死(MI)模型造模方法动物心梗模型还可以用于研究心梗与其他疾病的关系,如高*压、糖尿病等。这些疾病可能会加速心梗的发展。

对于使用动物进行研究的实验室,需要遵守相关的伦理和法律规定,包括动物福利法和实验动物管理规定等。标准化和规范化可以确保实验室符合这些规定,从而保证动物的福利和权益得到保护。除此之外,标准化和规范化可以促进研究结果的共享和交流,从而加速科学研究的进展。如果研究中使用的动物疾病模型没有标准化和规范化,那么其他研究人员可能无法重复这些实验或者比较不同实验之间的结果,从而影响科学研究的进展。综上所述,动物疾病模型的标准化和规范化对于确保研究结果的可重复性和可比性、保护动物的福利和权益以及促进科学研究的进展都非常重要。
动物疾病模型的选择对模型的有效性有很大的影响。不同的动物疾病模型具有不同的优缺点,因此选择合适的模型对于研究的准确性和可靠性至关重要。首先,选择合适的动物疾病模型可以提高研究的可重复性和可靠性。如果选择的模型与人类疾病的病理生理特征相似,那么研究结果更有可能在人类中得到验证。其次,选择合适的动物疾病模型可以提高研究的效率。如果选择的模型与人类疾病的病理生理特征相似,那么研究结果更有可能在人类中得到验证,从而减少了研究的时间和成本。除此之外,选择合适的动物疾病模型可以提高研究的可行性。如果选择的模型与人类疾病的病理生理特征相似,那么研究结果更有可能在人类中得到验证,从而增加了研究的可行性。综上所述,选择合适的动物疾病模型对于研究的准确性、可靠性、效率和可行性都有很大的影响。因此,在选择动物疾病模型时,需要考虑多方面的因素,以确保研究的有效性。通过小鼠心梗模型,可以观察到心梗后心肌细胞的改变、心脏功能的变化以及治*干预的效果。

动物心梗模型研究可以为我们提供深入了解心肌梗死发病机制的机会。通过模拟人类心梗的情况,研究人员可以在动物模型中观察到心肌缺血和心肌梗死的病理过程,从而更好地理解这些疾病的生物基础。 在动物心梗模型中,研究人员通常会采用手术或药物手段来阻塞动物的冠状动脉,以模拟人类心梗的发生。这种阻塞会导致心肌缺血,进而引发心肌梗死。通过对动物模型的观察和研究,研究人员可以了解心肌梗死的病理生理变化,包括心肌细胞的坏死、炎症反应以及心脏功能的改变等。通过TTC染色后,可以清晰地观察到心脏的梗死面积,为进一步的研究提供有力的支持。上海挤压心脏法心肌梗死(MI)模型
模型组HE染色部分心肌细胞核丢失、心肌细胞呈空泡样变、梗死区心肌细胞消失,代之以纤维瘢痕组织。上海挤压心脏法心肌梗死(MI)模型
小鼠心梗模型在心梗研究中的应用具有以下优点: 1. 模型制备相对简单:小鼠心梗模型的制备相对简单,且重现性较好,可以模拟不同类型的心梗,如前壁心梗、后壁心梗等。这为研究不同类型心梗的病因和发病机制提供了有利条件。 2. 成本效益高:与大型动物模型相比,小鼠模型的饲养和管理成本较低,且实验周期较短。这使得科研人员可以在较短的时间内获得大量数据,加速科研进程,提高研究效率。 3. 适用于药物筛选:小鼠心梗模型可以用于药物筛选,评估不同药物对心梗的治*效果。这为新药研发提供了有效手段,有助于筛选出具有潜在疗效的药物,为临床试验提供更多候选药物。 4. 有助于机制研究:小鼠心梗模型可以用于研究心梗的发病机制,通过观察不同时间点的病理变化,深入了解心梗的发展过程。这有助于揭示心梗的发病机制,为开发更有效的治*方法提供依据。 5. 适用于遗传学研究:小鼠具有丰富的遗传背景,可以用于研究遗传因素对心梗的影响。通过分析不同品系小鼠的心梗模型,可以深入了解遗传因素在心梗发*生、发展中的作用,为个性化治*提供依据。 上海挤压心脏法心肌梗死(MI)模型