- 品牌
- NSK,NTN,IBC,KBS,HRB,SYI,IKO
- 型号
- 6001ZZ
- 用途
- 风力发电机轴承,铁路轴承,仪器仪表轴承,汽车轴承,医疗器械轴承,绝缘轴承,水利工程轴承,精密机械轴承,万向节轴承,轧机轴承,通用轴承
- 材质
- 粉末冶金材料,塑料,轴承钢,铜合金,合金钢,不锈钢,铸铁
- 制式类型
- 公制轴承,英制轴承
- 尺寸标准
- 标准轴承,非标轴承
- 滚动体列数
- 单列轴承,双列轴承,多列轴承
- 组件能否分离
- 可分离轴承,不可分离轴承
- 能否调心
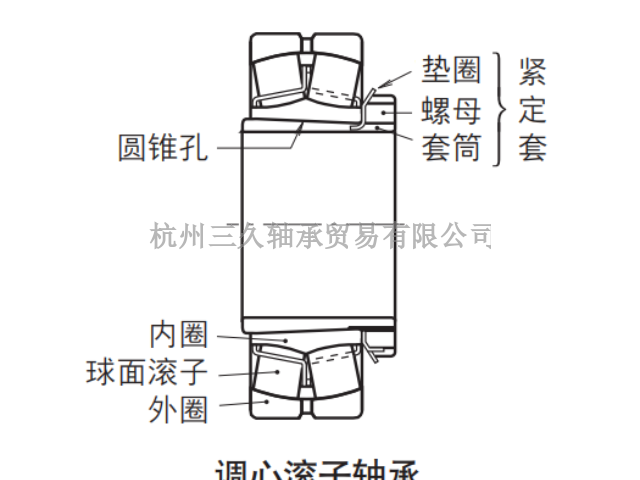
- 调心轴承,非调心轴承
- 使用特性
- 耐腐蚀,真空,低温,高温,高速
- 滚道类型
- 直线滚道,深沟滚道,球面滚道
- 保持架及其材料
- J钢板冲压,陶瓷合金,球墨铸铁
- 滚动体类型
- 球面滚子,圆锥滚子,圆柱滚子,滚针,球
- 样品或现货
- 样品,现货
- 加工定制
- 否
滚动轴承是极精密的机械元件,因此,不能忽视因温度引起的任何尺寸精度变化。相应地,根据规定,必须在 20°C 条件下进行轴承测量,且标准中规定的尺寸也是 20°C 时的值。温度变动引起的尺寸变化不仅影响尺寸精度,还会在运转时影响轴承的内部游隙。尺寸变化可能会引起内圈和轴或外圈和轴承座孔之间的过盈量变化。另外,还可以利用温差引起的尺寸变化,对过盈量大的零部件进行热装。温升导致的尺寸变化D l可通过以下公式 (8.11) 表示 :D l = DT a l (mm) ................................... (8.11)式中, D l : 尺寸变化 (mm)D T :温升 (°C)a : 轴承钢线性膨胀系数 a=12.5×10–6 (1/°C)l : 原始尺寸 (mm)轴承其承受载荷的方向可分为向心轴承和推力轴承。686轴承
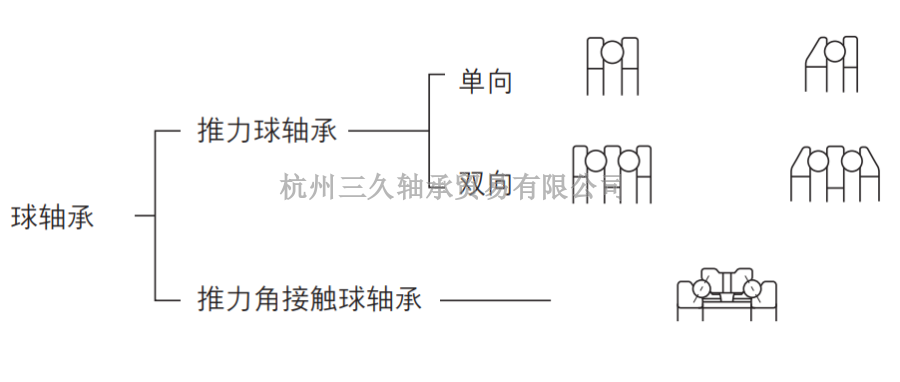
从另一个方面来说,如果将较低值或最小值作为标准,那么太多轴承的寿命又都会远超过该设定值。从这个观点来看,选择 90% 的值是出于惯例。其实,本来可以采取统计学上常用的 95%作为基准。不过,之所以根据经验选择较为宽松的90% 可靠性作为轴承的标准却有其实用和经济方面的考量。然而,如今,飞机、电脑和通信系统等应用并不采用 90% 可靠性,一些情况下,甚至会要求 99% 或 99.9% 的可靠性。图 4.27 显示了一组相同的轴承在相同条件下运行时的疲劳寿命分布情况。可使用韦氏方程描述10%~60% 失效概率(剩余概率 90%~40%)范围内的疲劳寿命分布。R2ZZ轴承单列角接触球轴承一般采用钢板冲压保持架。
当量动载荷一些情况下,作用于轴承的载荷*为单一径向载荷或单一轴向载荷。不过,大多情况下,多是这两种载荷组成的联合载荷。其方向、大小上也会变动。在此类情况下,实际作用于轴承的载荷不能直接用于计算轴承的寿命。所以,就要假想一个能保证与轴承在实际载荷和旋转条件下取得相同寿命、大小恒定且通过轴承中心的载荷。这种假想载荷叫做当量动载荷。当量动载荷的计算向心轴承的当量动载荷,可通过以下公式求出:P = XFr + YFa .......................................... (4.43)式中, P : 当量动载荷(N),{kgf}Fr : 径向载荷(N),{kgf}Fa : 轴向载荷(N),{kgf}X : 径向载荷系数Y : 轴向载荷系数X 及 Y 值列于轴承尺寸表中。α=0° 的向心滚子轴承的当量动载荷为P = Fr
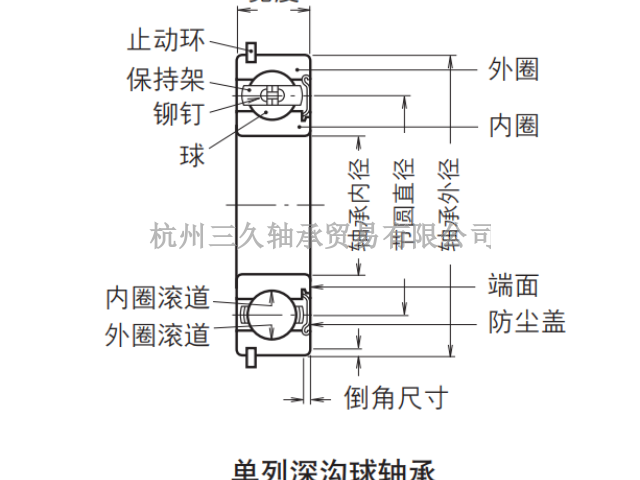
市场对各种使用滚动轴承的机械设备、仪器等的性能要求日趋严格,对轴承要求的条件、性能也日趋多样化。为了能从众多的结构、尺寸中选择**适合的轴承,需要从各种角度研究。在轴承选型时,通常,考虑作为轴系内的轴承配制、安装、拆卸的难易度、轴承占用的空间、轴承尺寸及轴承的市场性等,大致决定轴承结构。其次,通过比较研究各种使用轴承的机械的设计寿命和各种轴承的不同耐久程度,从而决定轴承尺寸。在轴承选型时,往往只考虑轴承的疲劳寿命,但由润滑脂老化而引起的润滑脂寿命、磨损、噪声等也需要充分考虑。此外,还要根据不同用途对精度、游隙、保持架结构、润滑脂等提出特殊的设计要求。单列深沟球轴承,位于内、外圈上的沟道,其截面半径略大于球半径呈圆弧形。

在配置的轴承中,将一套作为固定端轴承,用于进行轴向定位固定。该固定端要选择可承受径向载荷和轴向载荷的轴承。固定端轴承之外的其他轴承必须为“自由端”轴承,*承受径向载荷以解决轴膨胀和轴收缩问题。如不解决温度变化引进的轴的伸缩,轴承会受到异常的轴向载荷,成为早期损坏的原因。自由端轴承,使用内外圈可分离、可轴向移动的圆柱滚子轴承(NU、N 型等)、向心滚针轴承等,这类轴承易于安装和拆卸。将非分离型轴承用于自由端时,一般外圈和轴承座采用间隙配合,与轴承一起吸收轴在运转中产生的膨胀。另外,还可以通过内圈和轴的配合面吸收。单列深沟球轴承摩擦力矩小,适于高转速、低噪音、低振动的场合。686轴承
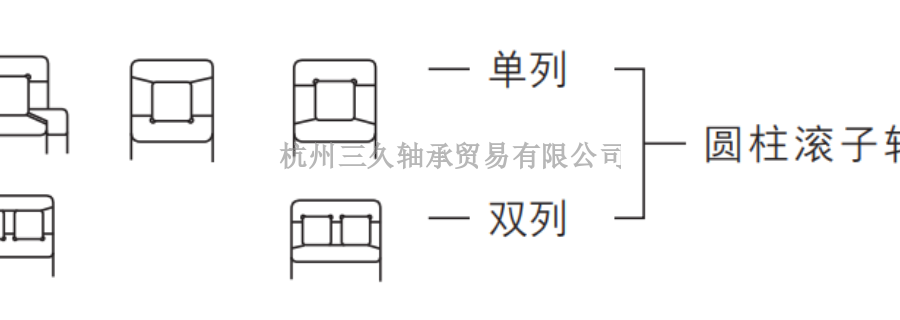
圆柱滚子轴承其具有高承载能力,适用于高速旋转应用。686轴承
内部游隙与规格数值:运转过程中,滚动轴承内部游隙的大小对疲劳寿命、振动、噪声、发热等轴承性能影响很大。因此,在确定类型和尺寸后,选择轴承内部游隙便是轴承选择**重要的任务之一。轴承内部游隙是轴承内 / 外圈和滚动体之间的组合间隙量。所谓径向游隙和轴向游隙,即内圈或外圈一方固定,另一套圈相对其在径向和轴向上的移动量。为了获得精确的测量结果,通常会向轴承施加规定的测量载荷来测量游隙。因此,测出的游隙值(为了区别,有时也称为“测量 游隙 ”)总是比理论内部游隙(向心轴承也称“几何游隙”)大出测量载荷造成的弹性变形量。686轴承
- 浙江NSK23134CE4C3S11轴承多少钱 2024-12-03
- 浙江NSK2313轴承批发 2024-12-03
- 浙江NSK24134CE4S11轴承卖价 2024-12-03
- 浙江NSK29412E轴承代理商 2024-12-03
- 杭州轴承型号查询尺寸大全 2024-12-03
- NSK24028CE4C3S11轴承零售 2024-12-03
- 浙江NSK120TAC03DT85SUELPN01轴承价格多少 2024-12-03
- 浙江NSK2306轴承大概价格 2024-12-02
- 浙江NSK2307K轴承具体参数 2024-12-02
- 杭州NSK24032CE4C3S11轴承代理价格 2024-12-02
- 浙江NSK23132CAMKE4S11轴承价格多少 2024-12-02
- 浙江NSK23126CAME4S11轴承尺寸 2024-12-02